(23.03.20-22)
읽기 및 구성 알고리즘 S. Dasgupta, CH Papadimitriou 및 UV Vazirani(2008)
http://algorithmics.lsi.upc.edu/docs/Dasgupta-Papadimitriou-Vazirani.pdf
조직
5.1 최소 스패닝 트리
-> Kruskal의 알고리즘
그리디 알고리즘
매 순간 최선의 선택을 하는 방법이지만, 매 순간 최선의 선택이 궁극적으로 최선의 선택이라는 보장은 없습니다.
위에서 아래로 최선의 선택을 하는 것입니다.
다시 말해서:
“솔루션 세트에 포함할 다음 항목을 선택하십시오.모두. 우리는 모든 단계에서 최적의 선택을 합니다.”
“국부적으로 최적의 솔루션을 찾아 최종적으로 글로벌 최적 솔루션을 찾는 방법”
-> 최종 선택이 전체적으로 100% 최적이라고 할 수 없습니다.
그러나 그리디 알고리즘을 사용하여 최적의 솔루션을 도출하는 데에는 문제가 있습니다. (크루스칼 알고리즘)
신나는 나무
– 연결된 무방향 그래프, 비순환
무방향 그래프의 최소 연결 그래프라고 할 수 있습니다. 다이어그램에서 일부 가장자리를 선택하여 만든 트리!!
– 스패닝 트리는 모든 정점이 포함되어 있고 모든 정점이 연결되어 있으며 이들을 연결하는 간선의 수가 최소인 그래프입니다.
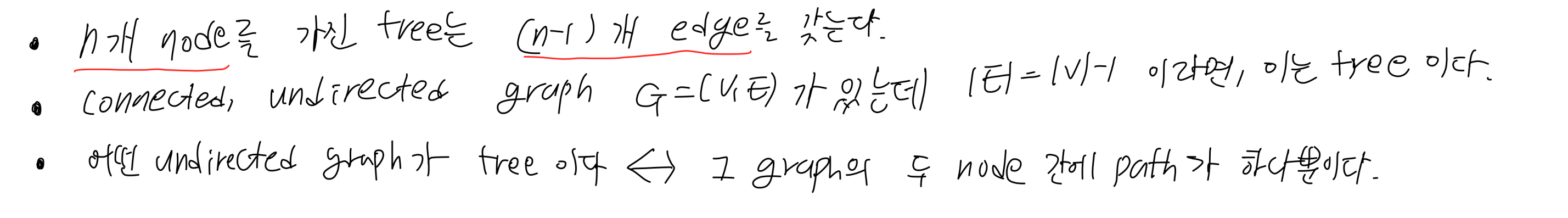
최소 스패닝 트리
– 스패닝 트리 중 에지 가중치의 합이 최소화되는 트리를 의미한다.

크루스칼의 최소 스패닝 트리 알고리즘
– 최소한의 비용으로 네트워크의 모든 노드를 탐욕적으로 연결하는 최적의 솔루션을 찾는 알고리즘오전.
—> 이 방법은 빈 다이어그램에서 시작하여 E의 가장자리를 선택하여 최종 트리를 완성합니다.
– 에지를 선택하는 조건은 가장 밝은하다, 자전거를 타지 마세요 가장자리입니다.
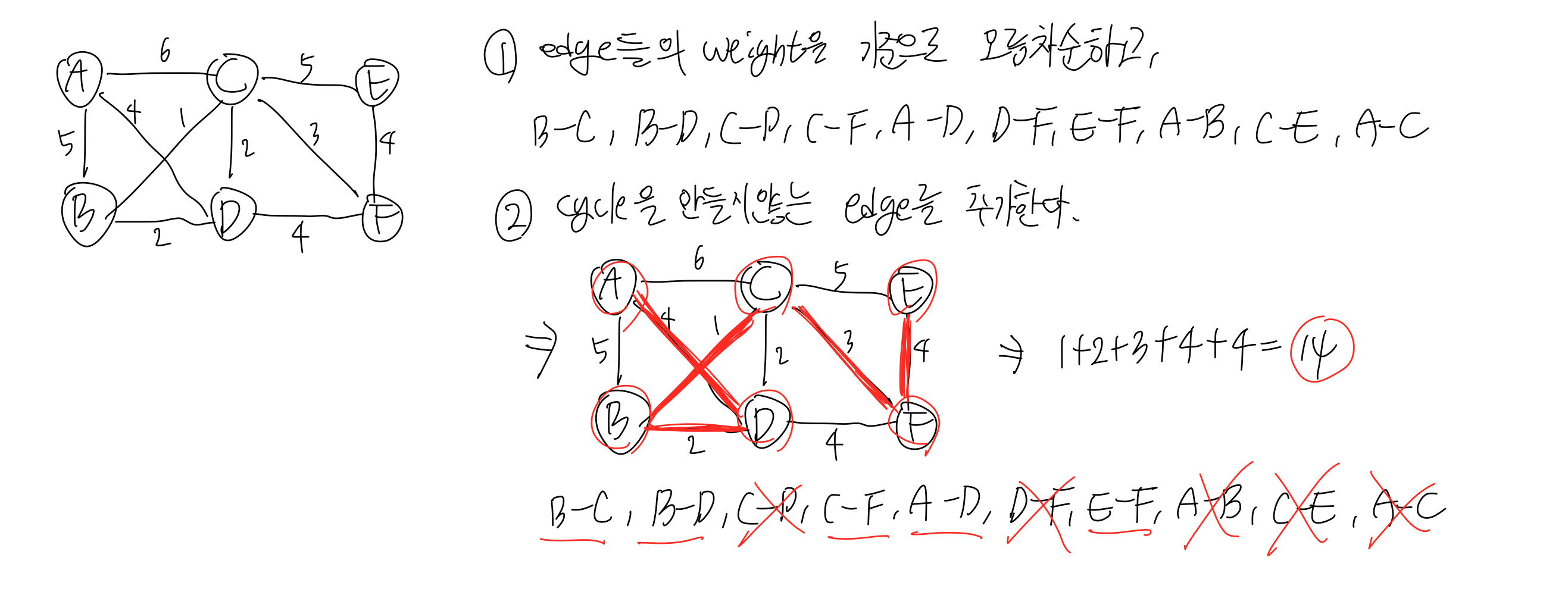
Kruskal의 최소 스패닝 트리 알고리즘의 작동 단계
1) 가중치의 오름차순으로 모서리를 정렬합니다.
2) 오름차순으로 정렬된 모서리를 하나씩 선택하므로 주기가 없습니다.
3) 선택한 에지가 최소 비용 스패닝 트리(MST) 세트에 추가됩니다.
—> 여기에서 Kruskal 알고리즘의 정확성이 입증됩니다. 절단 속성 오전.
—> 주기가 생성되지 않았는지 확인하는 방법: 유니온 찾기
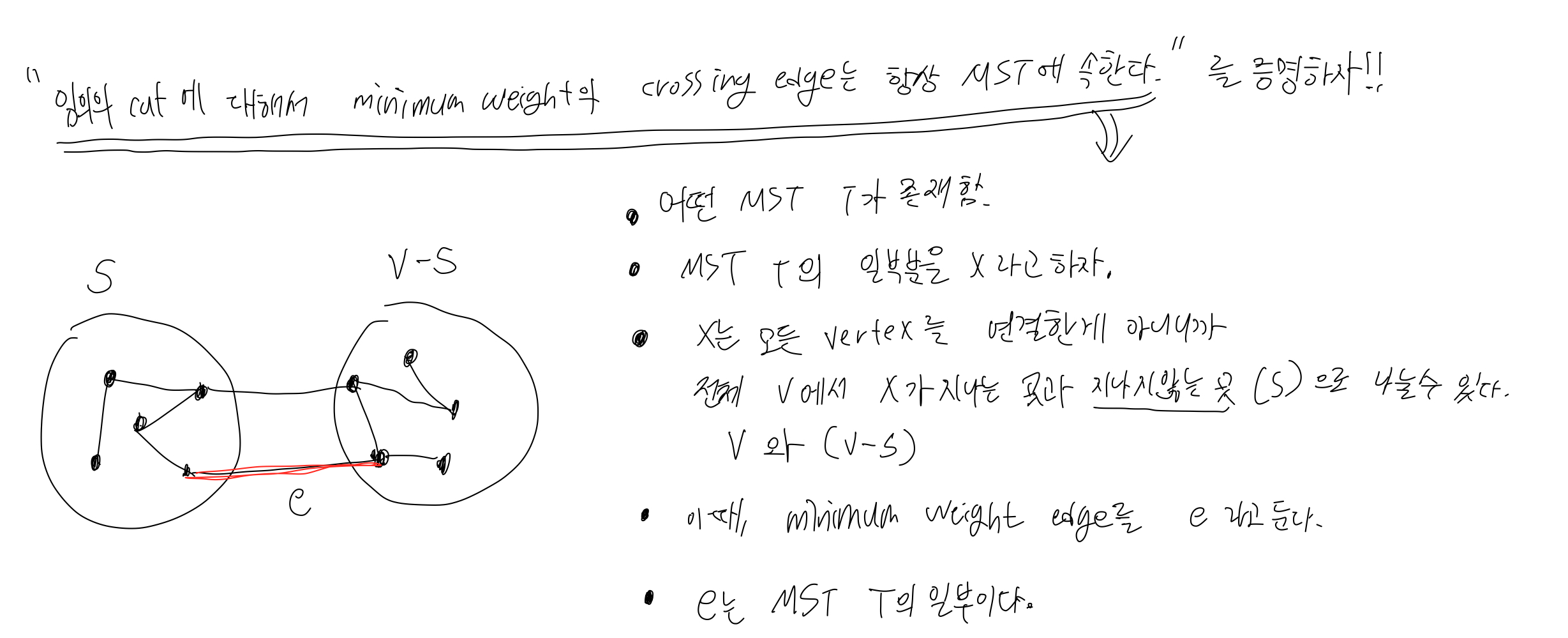
컷 속성
컷은 두 세트로 나누어진 정점 세트입니다.
각 세트의 노드로 연결된 모서리를 교차 모서리라고 합니다.
절단 특성은 최소한의 무게를 가진 절단면이 항상 절단할 때마다 MST에 속한다는 것입니다.
(명백한 것을 증명하려고 하기 때문에 어렵습니다)

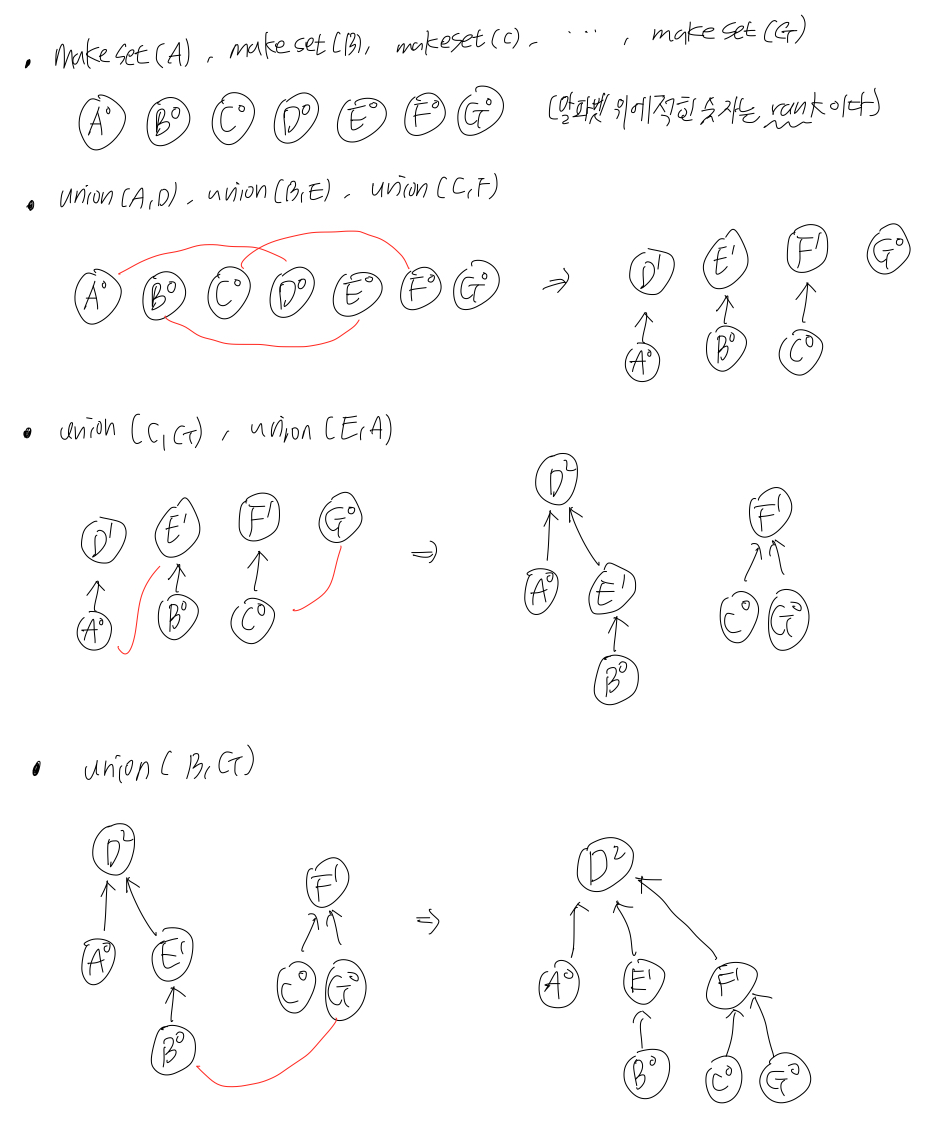
유니온 찾기
: 순환의 형성 여부를 판단할 수 있는 데이터 구조
Kruskal의 알고리즘은 edge (u,v)를 선택할 때 u와 v를 다른 구성요소에서 선택하고 선택 후 u가 속한 구성요소와 v가 속한 구성요소를 결합합니다. -> 유니온 찾기에는 그런 기능이 있습니다.
makeset(x): x 요소만으로 집합을 만듭니다.
find(x): x가 속한 집합 찾기
union(x, y): x가 속한 집합과 y가 속한 집합을 병합합니다.

find(u)와 find(v)가 같지 않으면 집합을 결합하기 위해 union(u, v) 연산이 수행됩니다.
( |V| makeset, 2|E| 찾기, |V|-1 합집합 연산)
Union-Find는 각 세트를 지시된 트리로 구현합니다.